Rabinowicz and Strömberg on Hare's universalizability argument for utilitarianism

Recently, I wrote up some thoughts about how we might give a contractualist argument for either utilitarianism or prioritarianism. The rough idea is this: For the contractualist, the moral value of a world in which welfare is distributed across a set of individuals in a particular way should be some sort of compromise between the different levels of welfare, and in particular a compromise that each of those individuals can reasonably accept. I made that suggestion precise by saying that it should be a value whose total deviation from each of the welfare levels should be minimal. Each individuals recognises that, if different individuals have different levels of welfare, the social chooser must use a measure of the moral value of the distribution that deviates from the welfare level of at least some of them. But they can reasonably require that it deviates from theirs no more than is necessary. And I showed that, for some measures of distance, we get the utilitarian’s measure of moral value—namely, the average of the welfare levels—and for other measures of distance, we get the prioritarian’s measure of moral value—namely, the average of the priority-adjusted welfare levels, which are some concave function of the welfare levels.

David McCarthy then pointed me to a suggestion by Wlodek Rabinowicz and Bertil Strömberg that uses a similar idea, but for a rather different purpose. Rabinowicz and Strömberg are interested in plugging a gap in Richard Hare’s argument for preference utilitarianism.

Richard M. Hare (1919-2002)

To sketch Hare’s argument, imagine a situation in which I must choose between two acts, both of which affect me and another individual, Ada. There is no uncertainty involved, and so we know the outcomes of each of the two acts. The outcome of the first has utility 8 for me, 2 for Ada; the outcome of the second has utility 3 for me, 5 for Ada—for Hare, what I’m calling utilities are strengths of preference. Let’s write the first as (8, 2) and the second as (3, 5). The crucial assumption of Hare’s argument is that whatever your moral judgment about which is better, it should be universalizable. That is, you should make the same judgment about the situation in which your roles are reversed, which we write (2, 8) vs (5, 3). Now Hare writes:

if I have full knowledge of the other person’s preferences, I shall myself acquire preferences equal to his regarding what should be done to me were I in his situation; and these are the preferences which are now conflicting with my original prescription. So we have in effect not an interpersonal conflict of preferences or prescriptions, but an intrapersonal one; both the conflicting preferences are mine. I shall therefore deal with the conflict in exactly the same way as with that between two original preferences of my own. (Hare, 1981, 108ff)

It sounds like what Hare means is this: I prefer (8, 2) to (3, 5) because I get more utility from that option; but I prefer (5, 3) to (2, 8) because I get more utility from that option. But these are in conflict, because they are different preferences concerning two situations that are really the same situation but with the roles switched. And so I resolve this conflict in the way I would any internal conflict between my assessments of a single situation; that is, I average the utilities involved, so that my moral value for the outcome of the first act is (8+2)/2=5 and for the second act is (3+5)/2=4. Hare thinks that this is what I would do were the conflict between preferences of my own. Indeed, he thinks that by considering myself in Ada’s shoes, I in fact take on her preferences as my own and so need to resolve the conflict in the way I would normally do.

Now, let’s set aside for the moment the question of whether we really do or should resolve internal conflicts as Hare describes—I’ll return to that at the end. Still, as Fred Schueler and Ingmar Persson point out, there is a gap in Hare’s argument, for the situations (8, 2) vs (3, 5) and (5, 3) vs (2, 8) are not in fact the same situation: in one, I take my own place; in the other, I take Ada’s. And so there is no conflict that needs to be resolved, and so no requirement to resolve it using our intrapersonal technique of averaging.

Nonetheless, Rabinowicz and Strömberg point out, there is a need to do something because the universalizability requirement that is really the central premise in Hare’s argument says that I must make the same assessment concerning (8, 2) vs (3, 5) as (2, 8) vs (5, 3). So the problem is not that there is an internal conflict between my assessments of the same situation; rather, there is a conflict between my assessments of different situations that the universalizability requirement rules impermissible.

Rabinowicz and Strömberg take the universalizability requirement to entail that we must have a value u that we assign to the first act whether we take our own position in that situation or Ada’s, and a value v we assign to the second act whether we take our own position or Ada’s. How are we to set these values u and v? This is where Rabinowicz and Strömberg’s suggestion makes contact with my contractualist argument for utilitarianism. They suggest we should pick u so that the welfare distribution (u, u) is as close as possible to (8, 2), and you should pick v so that the welfare distribution (v, v) is as close as possible to (3, 5). The idea is that, in satisfying the universalizability requirement, you should move as little as possible from your utilities in the two situations: 8 for the first act when you occupy your own place and 2 for the first act when you occupy Ada’s; and similarly for the second act.

But as close as possible relative to which measure of distance? Rabinowicz and Strömberg focus on the Euclidean distance measure, so that the distance between (a, b) and (c, d) is the square root of the sum of the squared differences between a and c and b and d. That is:

\(\mathrm{Euc}((a, b), (c, d)) = \sqrt{(a-c)^2 + (b -d)^2}\)

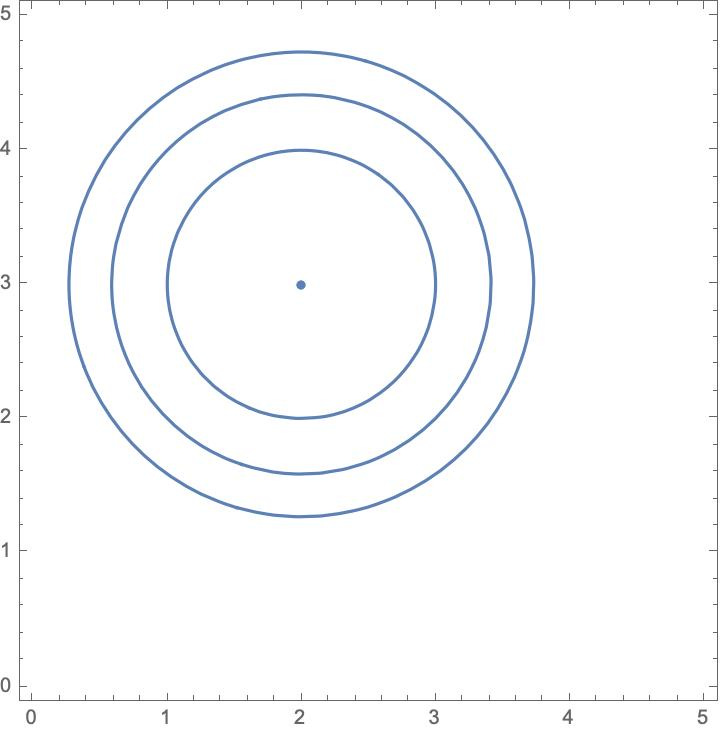
And they note that, using this measure of distance, for any (a, b), the distance from (u, u) to (a, b) is minimized by the average of a and b. That is:

\(u = \frac{a+b}{2}\)

And the result generalizes to any number of individuals. From this, average utilitarianism follows.

Each closed curve shows a set of points equally far from the point (2, 3) relative to the Euclidean distance measure Euc.

I don’t want to question here any of the philosophical aspects of Rabinowicz and Strömberg’s reconstruction/adaptation of Hare’s argument. They’re fascinating and I think worth a lot of attention, which I’d like to leave for another time. What I hope to do here instead is point out that using other well-known measures of distance gives rather different conclusions.

For instance, here is a measure of distance between two welfare distributions that Imre Csiszár calls the I-divergence (it is a generalization of a well-known measure of distance between probability functions known as the Kullback-Leibler divergence, which is central to information theory):

\(\mathrm{Idiv}((a, b), (c, d)) = a\log \frac{a}{c} - a + c + b\log \frac{b}{d} - b + d\)

The first thing to note is that the I-divergence is not symmetrical: that is, for many pairs, the divergence from the first to the second will be different from the divergence from the second to the first. This means that, in order to carry out Rabinowicz’s procedure, we must decide whether we should minimize divergence from (u, u) to (a, b) or from (a, b) to (u, u). And it turns out that they give different results. If we minimize the divergence from (a, b) to (u, u), we get u = (a+b)/2, as we did for Euclidean distance. If we minimize divergence from (u, u) to (a, b), we get something different. In fact, we get:

\(u = e^{\frac{\log a + \log b}{2}}\)

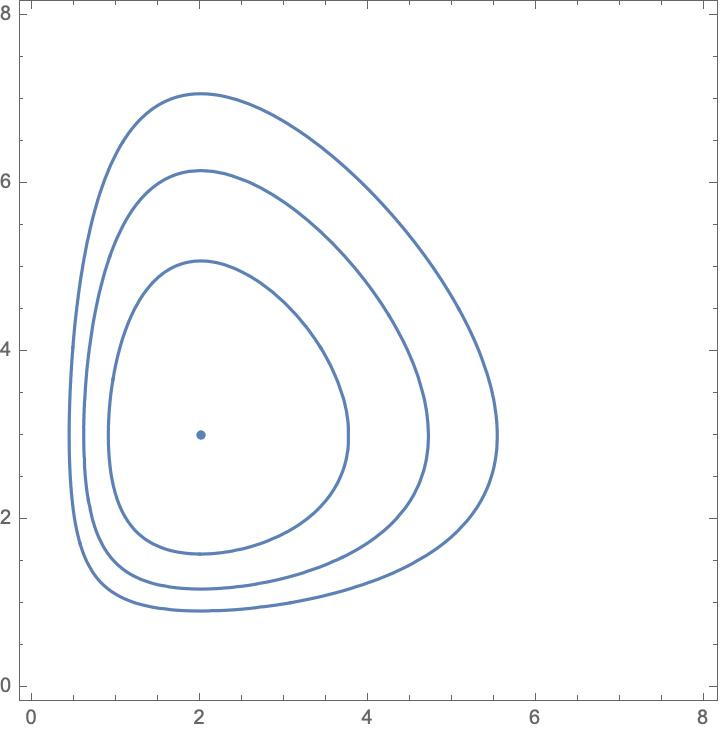
This is interesting, because it is a version of prioritarianism. The standard version of (average) prioritarianism says that the value of a welfare distribution (a, b) is the average of the priority-adjusted levels of welfare it contains. We adjust the welfare of an individual by applying a concave function f to it, so that the average priority-adjusted welfare of (a, b) is (f(a) + f(b))/2. This ensures that, the lower an individual’s level of welfare, the greater the increase in moral value achieved by increasing their welfare by a fixed amount. Let’s take our priority-adjusting function to be the logarithmic one—that is, f(x) = log x. Then the average prioritarian value for (a, b) is the average of log a and log b. But if we leave it at that, the view is vulnerable to a famous objection by Alex Voorhoeve and Mike Otsuka. But, as Marc Fleurbaey showed, we can avoid that objection if we take the average prioritarian value for (a, b) and apply the inverse of the priority-adjusting function—in this case, the exponential function. And that gives us the same value as we get above by minimizing the I-divergence from (u, u) to (a, b).

Each closed curve shows a set of points equally far from (2, 3) relative to the I-divergence, Idiv.

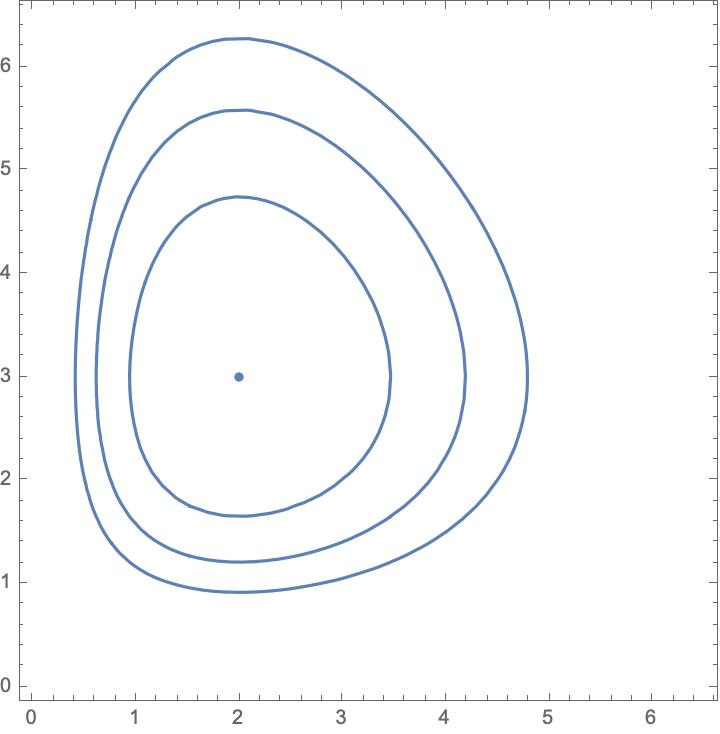
We get other versions of prioritarianism by choosing other concave functions as our priority-adjusting functions. And, for many of them, there are divergences like the I-divergence that will give rise to those using Rabinowicz and Strömberg’s procedure. The so-called Hellinger distance, for instance, gives prioritarianism with the square root function as its priority-adjusting function.

\(\mathrm{Hell}((a, b), (c, d)) = (\sqrt{a} - \sqrt{c})^2 + (\sqrt{b} - \sqrt{d})^2\)

And, relative to this, minimizing distance from (a, b) to (u, u) gives:

\(u = \left (\frac{\sqrt{a} + \sqrt{b}}{2} \right )^2\)

I discuss a few others in these notes. And I describe there some of the properties that tell between these different measures of distance. For it is by looking at those that we will be able to tell whether utilitarianism or prioritarianism or something different altogether is correct.

Each closed curve shows a set of points equally far from (2, 3) relative to the Hellinger distance.

Let me close by returning to Hare’s claim, made in the midst of his argument for utilitarianism, that when we resolve intrapersonal conflicts between our own different assessments of the same outcome, we split the difference between those assessments and take the average utility. The foregoing, I think, casts doubt on even that claim. After all, when we resolve that sort of conflict, we want to do the same sort of thing that Rabinowicz and Strömberg describes: we want to give a value that doesn’t lie unnecessarily far from any of the conflicting values we’re attempting to resolve. And so we measure the total distance from the candidate compromises to the conflicting values and we pick the one for which this is minimal. But, as we can see, different choices of distance measure give different ways of effecting that compromise. Some give the average, as Hare demands, but others don’t. So perhaps we should not be utilitarians when weighing up the utilities assigned by our different selves across time; perhaps we should be prioritarians of some stripe.