25 years of accuracy-first epistemology - Part 1

Jim Joyce's nonpragmatic vindication of probabilism

Twenty-five years ago, in December 1998, Jim Joyce’s ‘A Nonpragmatic Vindication of Probabilism’ was published in Philosophy of Science. And exactly a year earlier, Graham Oddie’s ‘Conditionalization, Cogency, and Cognitive Value’ was published in The British Journal for the Philosophy of Science. Together, these papers launched the position in epistemology that has come to be known as accuracy-first or accuracy-centred epistemology, or sometimes epistemic utility theory or cognitive decision theory. To mark this 25th-ish anniversary, I thought I’d try to spell out a little of what’s going on in those papers and what has been built on them since. I’ve written a longer overview of the topic for the Stanford Encyclopedia of Philosophy, and Jonathan Weisberg has a nice set of introductory blogs, but I thought it might be valuable to work through some of the papers that comprise this literature.

While Oddie’s paper came out first, I’ll begin with Joyce’s, since the conclusion it hoped to establish is in some sense prior to the conclusion Oddie seeks.

The highly accurate James M. (Jim) Joyce

What is Probabilism?

So what is that conclusion? It is the norm of Probabilism from Bayesian epistemology, and I will begin by explaining what that is.

Probabilism is a norm or law of rationality that governs your degrees of belief or credences. So, first, what are degrees of belief or credences? Ask me how confident I am that I switched off the lights before I left my flat and I’ll say something like ‘95%’. When I do that, I report my credence in the proposition that I switched off the lights. This credence measures how strongly I believe the proposition. The first tenet of Bayesian epistemology is that our degrees of belief, or credences, can be represented in this way by precise numerical values that lie between 0 or 0%, which represents the lowest possible credence I can assign, and 1 or 100%, which represents the highest possible credence I can assign.

The second tenet of Bayesian epistemology is Probabilism, which tells us something about how our credences should be. It tells us first that necessarily true propositions should receive the maximal credence of 1 or 100%, while necessarily false ones should receive the minimal credence of 0 or 0%.¹ So your credence that 2+2=4 should be 100% and your credence that 3+7=9 should be 0%. This part of the norm is sometimes known as Normality. Probabilism tells us secondly that, if two propositions can’t both be true together, then your credence that one or other is true should be the sum of your credence that the first is true and your credence that the second is true. So your credence that I’m in Dundee or Dumfries should be the sum of your credence that I’m in Dundee and your credence that I’m in Dumfries. This part of the norm is sometimes known as Additivity. Probabilism is the conjunction of Normality and Additivity.

Probabilism has lots of natural consequences: (i) if one proposition is stronger than another, so that the first entails the second, then your credence in the first should never exceed your credence in the second—so you shouldn’t be more confident that I’m in Dundee than you are than I’m in Dundee or Dumfries; (ii) your credence in a proposition and your credence in its negation should add up to 100%—so if your credence I’m in Dundee is 54%, then your credence I’m not in Dundee should be 46%; (iii) if you have a whole string of propositions no two of which can be true together, then your credence in their disjunction should be the sum of your credences in each individual proposition—so your credence I’m in Scotland should be the sum of your credence I’m in Caithness, your credence I’m in Moray, your credence I’m in Bute, and so on through all the Scottish shires.

Probabilism looks simple, but in conjunction with the other tenets of Bayesian epistemology, it is remarkably powerful, allowing us to represent our uncertainty about any topic in a particular way and then telling us how that uncertainty should behave. It is really the foundation for many many representations of uncertainty in contemporary science.

The third and final tenet of the standard, subjective version of Bayesian epistemology, is Conditionalization or Bayes’ Rule, which tells you how your credences should evolve as new evidence arrives. I’ll come to that in the next post, since it is that norm that gives the conclusion of Oddie’s paper.

Pragmatic vindications of Probabilism

So now we have Probabilism, a norm that says what rationality requires of your degrees of belief, or credences. What is Joyce’s interest in it? Well, he wants to establish it. He wants to give an argument that shows that Probabilism is a genuine requirement of rationality; he wants to show that someone who is only 95% confident that 2+2=4 is irrational, as is someone who is 3% confident that 7+9=13, as is someone who is 76% confident I’m in Dundee but only 43% confident I’m either in Dundee or in Dumfries, and so on. And yet there were arguments to this conclusion before December 1998. So how does Joyce’s argument fit in with those? Those arguments, he tells us, are pragmatic arguments, while his is not, as the article’s title suggests.

To see what he means, let’s go through two of those arguments. As we’ll see, the second is in fact a source of inspiration for Joyce.

The first pragmatic vindication

The first pragmatic argument for Probabilism—typically known as the Dutch Book argument or the betting argument or the sure loss argument—originates, as does so much, from Frank P. Ramsey’s astonishing essay, ‘Truth and Probability’, written in 1926 and first published posthumously in 1931 in the volume of his work that R. B. Braithwaite edited.² A fuller formulation was offered independently by Bruno de Finetti, to whom we owe also the second pragmatic argument we’ll consider, in his ‘Foresight: Its Logical Laws, Its Subjective Sources’.³

The central idea is that your credences should guide your choices in particular ways, and if your credences aren’t as Probabilism says they should be, there will be a series of decisions you might face such that your credences require you to choose in a particular way when faced with each decision, but there is an alternative sequences of choices you could have made instead that, taken together, would have been better for sure than the sequence of choices your credences require you to make, when they’re taken together.

More precisely, the first premise is what I’ve called elsewhere Ramsey’s Thesis. Suppose your credence in a proposition is x%. Now consider a bet that pays out a certain amount, say £n, if that proposition is true and nothing if it’s false. Ramsey’s Thesis says you should be willing to pay anything under x% of £n to buy that bet, and you should be willing to take anything over x% of £n to sell that bet. So, for instance, if you’re 63% confident that you turned off the lights, you’ll buy a £10 bet on that for anything under £6.30 and you’ll sell it for anything over £6.30.

We then appeal to the so-called Dutch Book Theorem, which shows that, if your credences aren’t as Probabilism says they should be, then there is a sequence of bets, each with a price attached and an indication whether you’ll be offered to buy it or sell it, such that (i) for each bet in the sequence, your credences require you to buy or sell it, whichever is indicated, at the attached price, and (ii) taken together, this sequence of bets is guaranteed to lose you money, that is, it subjects you to a sure loss, that is, taken together, you lose money however the world turns out to be, so that you’d have been better off for sure to reject each bet. For instance, suppose you’re 80% confident I’m in Dundee but only 50% confident I’m in Dundee or Dumfries. Then (1) you’ll buy a £10 bet that I’m in Dundee for £7, and (2) you’ll sell a £10 bet that I’m in Dundee or Dumfries for £6. So you’ve paid out £7 and taken in £6, so you’re £1 down before the bets are settled. Now, if I’m in Dundee, when the bets are settled, you’ll win £10 from bet 1 and have to pay out £10 from bet 2, so you’ll stay £1 down; if I’m in Dumfries, you’ll win nothing from bet 1 and pay out £10 from bet 2, so you’ll now be £11 down; and if I’m in neither, you’ll win nothing from bet 1 and nothing from bet 2, and so you’ll stay £1 down. That covers all the cases, and so you’re credences require you to make a sequence of choices that lead you to lose money for sure. And, what’s more, if only your credences had behaved as Probabilism tells them to, this wouldn’t have been possible: the so-called Converse Dutch Book Theorem says that, if your credences do as Probabilism says, then there is no series of bets with attached prices and indications whether to buy or sell such that (i) for each bet in the sequence your credences require you to buy or sell it, whichever is indicated, at the attached price, and (ii) taken together, this sequence of bets is guaranteed to lose you money. And that, the Dutch Book argument claims in its third premise, makes credences that don’t obey Probabilism irrational.

This argument is pragmatic because it seeks to establish the norm of Probabilism, which governs our beliefs, by looking at the choices they lead us to make and the goods that they get for us or fail to get for us.

The second pragmatic vindication

De Finetti’s second pragmatic argument also seeks to establish Probabilism by looking at the choices our credences lead us to make and their outcomes—indeed, this is what makes it a pragmatic argument. In the Dutch Book argument, the choices you face depend on the credences you have; in de Finetti’s scoring argument, everyone faces the same choice. You must choose which credence you should report yourself as having. I will then score that credence, and penalize you based on that score. Your aim, of course, is to minimize your penalty. How will I score you? For each proposition, I’ll take the credence you report in that proposition; if the proposition is false, I’ll take the square of your reported credence and penalize you by that amount; if the proposition is true, I’ll subtract your reported credence from the maximum possible credence, square that, and penalize you by that amount. So, if your reported credence that I’m in Dundee is 60%, or 0.6, and I’m not in Dundee, I’ll score you 0.36, which is the square of 0.6; and if I am in Dundee, I’ll score you 0.16, which is the square of 1-0.6, i.e., 0.4. This means of scoring is now known as the Brier score, named for the meteorologist Glenn W. Brier, who proposed using it to score the probability reports of weather forecasters.

De Finetti notes three features of this set-up:

• First, the scoring system he’s described is what is now known as strictly proper (or, as Oddie calls it, cogent). That means that it incentivizes me to report my true credences. So, if my credence that you’re in Dumfries is 45%, I minimize my expected loss by reporting that my credence in this proposition is 45%; if it’s 39%, I minimize my expected loss by reporting 39%; and so on.⁴

• Second, if my credences don’t behave as Probabilism says they should, then there are alternative credences I might have reported instead of reporting my own ones such that, however the world turns out, I would have ended up penalized less overall if I’d reported them.

• Third, if my credences do behave as Probabilism says they should, then there are no alternative credences I might have reported instead of reporting my own ones such that, however the world turns out, I would have ended up penalized less overall if I’d reported them.⁵

And so, again, credences that disobey Probabilism are guaranteed to get us less of what we want than we might have had, while credences that obey it don’t have that flaw. Again, this is taken to indicate that such credences are irrational.

A visual proof of de Finetti’s result

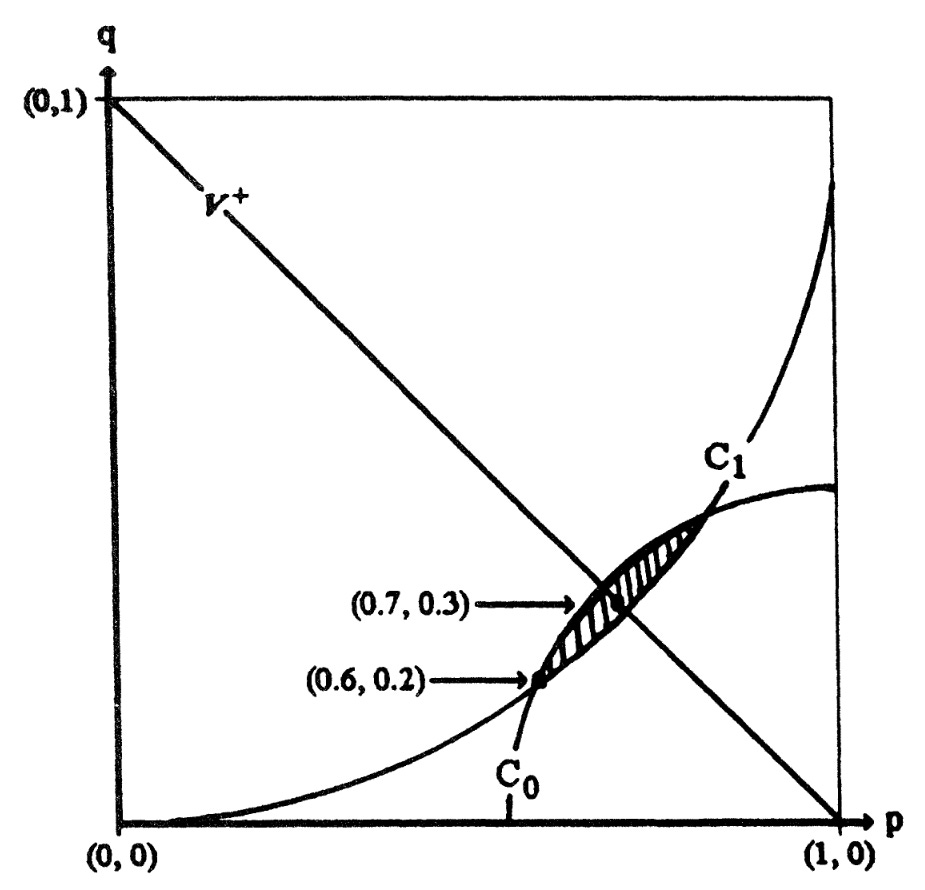
Indeed, in a diagram in his paper that has become a staple of presentations of accuracy-first epistemology, Joyce offers a visual demonstration of a particular case of de Finetti’s second point: he shows that, if your credence in a proposition and your credence in its negation don’t add up to 100%, then there are alternatives that are guaranteed to receive less penalty via the Brier score. Here’s the diagram:

Figure 1 from Joyce’s paper

In this diagram, we imagine someone who reports credences in a proposition X and its negation. We plot their reported credences in the unit square: so, if they report p as their credence in X and q as their credence not-X, then we represent them as the point (p, q). So, for instance, if you report 60% in X and 20% in its negation, then you’re represented by the point (0.6, 0.2) that is indicated by an arrow in the diagram.

Now, if you do report those credences, what is your penalty? If X is true, then it’s the square of 1-p plus the square of q. But, and this is the really crucial bit, this is just the square of the distance from the point (p, q) to the point (1, 0) at the bottom right.⁶ And (1, 0) represents what you might think of as the omniscient credences in the possible world in which X is true: it represents credence 100% in X and 0% in its negation. What’s more, if X is false, then the penalty for reporting (p, q) is the square of p plus the square of 1-q. And this time, this is the square of the distance from the point (p, q) to the point (0, 1) in the top left corner. And (0, 1) represents the omniscient credences in the possible world in which X is false: it represents 0% in the proposition and 100% in its negation. So the penalty imposed by the Brier score for reporting (p, q) at a possible world is just the square of the distance from the point (p, q) to the point that represents the omniscient credences at that world.

So let’s focus on (0.6, 0.2) again. If X is true, then the reported credences that receive a lower penalty than (0.6, 0.2) are those that are closer to (1, 0) than (0.6, 0.2) is. After all, if (p, q) is closer to (1, 0) than (0.6, 0.2) is, then the square of its distance from (1, 0) is less than the square of the distance of (0.6, 0.2) from (1, 0), and so its Brier score at the world at which X is true is less that the Brier score of (0.6, 0.2) at that world. And those reported credences are the ones that lie within the arc of the circle labelled C0 in Joyce’s diagram. On the other hand, if X is false, then the reported credences that receive lower penalty than (0.6, 0.2) are those that are closer to (0, 1) than (0.6, 0.2) is; and those are the ones that lie within the arc of the circle labelled C1 in Joyce’s diagram. Now, as we can see, there’s a shaded area that contains all reported credences that lie within the arcs of both circles C0 and C1. One of them, (0.7, 0.3), is labelled by another arrow. Each of them is guaranteed to receive a lower penalty than (0.6, 0.2) receives, just as de Finetti says.

The credences that obey Probabilism are the ones that lie on the straight diagonal line between (0, 1) and (1, 0) in Joyce’s diagram—for (p, q) on that line, p + q = 1, and so the credence in X and the credence in not-X sum to 1, just as Probabilism requires. It’s a reasonably straightforward geometric fact that, if (p, q) lies off that line, the arc of the circle centered on (0, 1) that passes through (p, q) intersects with the arc of the circle centered on (1, 0) that passes through it (p, q), and so there are credences that lie inside both arcs. And so there are alternative reported credences guaranteed to be penalized less.

Why a nonpragmatic vindication?

With two pragmatic vindications of Probabilism on the table, why do we need a nonpragmatic one? There are many reasons. First, there are the internal problems for the two pragmatic arguments just presented: (i) money has diminishing marginal value, so Ramsey’s Thesis is probably false; (ii) as Brian Hedden argues, even if you can find a quantifiable commodity that doesn’t have diminishing marginal value and use that in place of money in Ramsey’s Thesis, it isn’t obvious that someone whose credences don’t obey Probabilism should choose as Ramsey’s Thesis requires; (iii) as I’ve argued, even if Ramsey’s Thesis is true, all that the Dutch Book Theorem shows is that, if you don’t obey Probabilism, there is a sequence of bets each of which you should accept but that, taken together, leads to sure loss, and surely this isn’t sufficient to establish irrationality, since it doesn’t tell us how those credences perform as guides to action in the face of other sequences of decisions; and (iv) this same worry applies to de Finetti’s scoring argument, since again it only describes one situation in which things go wrong, and doesn’t give reason to think that credences that don’t satisfy Probabilism might not redeem themselves by the actions they prescribe in other situations.

However, Joyce’s own reasons don’t stem primarily from internal problems with the pragmatic arguments. Rather, he argues that the very fact that they are pragmatic is the problem. He quotes approvingly the following from Roger Rosenkrantz, who gave an early precursor to Joyce’s argument:

[the Dutch Book is a] roundabout way of exposing the irrationality of incoherent beliefs. What we need is an approach that ... [shows] why incoherent beliefs are irrational from the perspective of the agent’s purely cognitive goals.

I think one way to understand Joyce’s point, and Rosenkrantz’s, is this. Our credences play a number of different roles in our lives. They guide our actions, sure, and the pragmatic arguments show that those that disobey Probabilism play that role suboptimally (at least in very specific situations, such as when you face the sequence of bets described by the Dutch Book Theorem or de Finetti’s scoring decision). But they also serve to represent the world; they encode our uncertainty between different ways it might be. And it would be good to have an argument that shows that those that disobey Probabilism play that second role suboptimally. That is what Joyce seeks in this paper.

And, it turns out, he doesn’t need to look far for a prototype. For recall what we noted above about de Finetti’s argument: given a particular possible world, the penalty that the Brier score imposes at that world on the credences you report is just the square of the distance from those credences to the omniscient credences. So the further from the omniscient credences your reported credences lie, the greater the penalty you receive. And that sounds an awful lot like the sort of penalty we’d like to impose on your actual credences if we were assessing them by the extent to which they achieve your cognitive goals, to use Rosenkrantz’s phrase. After all, it is surely one of our chief cognitive goals to have credences that approximate as closely as possible the omniscient credences, which assign maximal credence to all truths and minimal credence to all falsehoods.

So the Brier score, when applied to your actual credences, might be seen as a measure of epistemic disutility; it measures the epistemic badness of a set of credences. And, having seen that, we can use de Finetti’s result: if your credences don’t do as Probabilism says they should, there are alternative ones you might have had instead that are guaranteed to lie closer to the omniscient credences, and so are guaranteed to have less epistemic disutility, and so more epistemic utility, than yours. And this begins to look like a nonpragmatic vindication of Probabilism.

This vindication begins with a claim about epistemic utility. That claim might be called Credal Veritism. It says that the sole fundamental source of epistemic utility for credences is their accuracy, that is, their proximity to the omniscient credences. The next step gives a measure of inaccuracy, namely, the Brier score. We might call the assumption that it is the correct measure of inaccuracy Brier Accuracy. The third step notes that, if you disobey Probabilism, then there are alternative credences that are guaranteed to be more accurate than yours. This is de Finetti’s theorem. And the fourth step claims that this renders you irrational: we might call this assumption The Dominance Principle, for it says that it is irrational to choose a dominated option, where one option dominates another if the former is guaranteed to be better than the latter. If you measure inaccuracy by the Brier score, de Finetti’s theorem shows that any credences that disobey Probabilism are accuracy-dominated.

Roughly speaking, this is the argument at which Roger Rosenkrantz gestured. But, as Joyce noted, it doesn’t quite work, for we have yet to say why we should measure inaccuracy using the Brier score; that is, we have yet to establish Brier Inaccuracy. A key contribution of Joyce’s paper is to note that we needn’t make that assumption. Rather, he lays down a whole bunch of properties we would like a measure of inaccuracy to have, and then he shows that de Finetti’s result goes through regardless of which one we choose. We might call the assumption that inaccuracy should be measured by a function that has all the properties Joyce lists Joycean Inaccuracy; and we might call the theorem he proves that generalizes de Finetti’s theorem Joyce’s Theorem. His argument then runs:

1. Credal Veritism

2. Joycean Inaccuracy

3. Joyce’s Theorem

4. The Dominance Principle

Therefore

5. Probabilism

The argument, in this form, has survived mostly intact for twenty-five years. The only difference is that accuracy theorists now tend to reject Joycean Inaccuracy. They replace it with the assumption that measures of inaccuracy have the very property that de Finetti noted of the Brier score, namely, that it’s strictly proper. So, we might call Strictly Proper Inaccuracy the assumption that a measure of inaccuracy should be strictly proper, that is, each set of credences that obeys Probabilism should expect itself to be less inaccurate than it expects any other set of credences to be, when we measure inaccuracy in this way. In 2009, Joel Predd and his collaborators showed that this is sufficient to give a version of Joyce’s argument. Call their result Predd et al’s Theorem. Then we have the following argument for Probabilism:

1. Credal Veritism

2. Strictly Proper Inaccuracy

3. Predd et al’s Theorem

4. The Dominance Principle

Therefore

5. Probabilism

This is what is now typically known as the accuracy dominance argument for Probabilism.

1. There are subtleties about the notion of necessity involved here, but I won’t try to adjudicate them. Things also get more nuanced if your background logic is not classical, but again, I won’t try to explain that.

2. The same Braithwaite whose poker features in the famous encounter between Ludwig Wittgenstein and Karl Popper at Cambridge.

3. For overviews of the Dutch Book arguments, see Susan Vineberg’s SEP article or my Cambridge Element.

4. You can prove this yourself with a little high school calculus. Suppose your credence in X is p. Then you want to pick x that minimizes the following quantity, which gives your expected penalty for reporting x as your credence in X:

\(p \times (1-x)^2 + (1-p) \times x^2\)

5. This is in fact quite a straightforward consequence of the fact that the scoring system is strictly proper. It’s fun to think through why!

6. Recall the definition of the Euclidean distance from one point to another: the Euclidean distance from (a, b) to (c, d) is

\(\sqrt{(a-c)^2 + (b-d)^2}\)